Октаэдр из бумаги, развертка, как сделать октаэдр самому из бумаги, схема для склеивания

Поделка посложнее

Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.

Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!

Статья по теме: Плетение из резинок: чехол для телефона крючком со схемами и видео

Основные виды

Икосаэдр, который можно изготовить из бумаги, может быть разным.

Например, если:

применять в работе бумагу только одного цвета, то фигура получится одноцветной;
это будет цветная бумага, можно сделать многоцветный икосаэдр, который будет играть разными красками и выглядеть более красиво.

Нередко изготавливают икосаэдр, внешне по расцветке похожий на футбольный мяч, когда белые треугольники чередуются с черными. В действительности это будет, не мяч, поскольку он далек от круглой формы. Более сложный в исполнении – икосаэдр, имеющий форму звезды. Здесь уже имеются грани, которые выступают вперед на фоне других.

Самым же красивым является икосаэдр, украшенный различными декоративными элементами. Это могут быть любые украшения: что-нибудь блестящее, яркое – то, что легко можно прикрепить к поверхности бумаги. Такой икосаэдр можно использовать в качестве новогодней игрушки и вешать на елку.

В геометрии существует бесчисленное количество икосаэдров. Часть из них имеют больше симметрий, а другие, наоборот, являются менее симметричными. Наибольшую распространенность имеет правильный икосаэдр – тот, где ровно 20 одинаковых граней. Правильным икосаэдром в математике может называться как выпуклое, так и невыпуклое тело.

В любом случае у каждого из них по 20 граней и в 1,5 раза больше ребер. У обоих так называемая иксосаэдральная симметрия. Однако зачастую правильным икосаэдром называют его выпуклую разновидность, тогда как невыпуклая форма попадает в категорию больших икосаэдров.

Икосаэдр (развертка для склеивания) может быть представлен следующими вариантами:

Фигура	Описание
Выпуклый икосаэдр	Он имеет 20 граней и 12 вершин. У этого геометрического тела есть двойственный многогранник. Он называется правильным додекаэдром. У него 3 правильные 5-угольные грани вокруг каждой вершины.
Большой икосаэдр	Он обладает ровно 20-ю гранями, каждая из которых является правильным треугольником. Однако его вершина – не 5-угольник, а пентаграмма. Именно по этой причине грани геометрически пересекаются. При их пересечении не образуется новых ребер. Двойственный многогранник большого икосаэдра – большой додекаэдр. У него вокруг каждой вершины сосредоточено по 3 грани, каждая из которых представляет собой 5-угольник.
Звездчатые икосаэдры	Если грани или ребра многогранника расширяются, то при их соприкосновении образуется звездчатая форма. Это происходит симметрично, поэтому получившееся тело имеет те же симметрии, что и у исходных фигур. В научном труде Коксетера «59 икосаэдров» перечислено почти 60 звездчатых разновидностей этих многогранников. Многие из них обладают отдельной гранью, в каждой из 20 плоскостей. У многих других тел свыше 1-й грани на плоскости. Они могут быть образованы при слиянии более простых многогранников.
Псевдоикосаэдр	Правильный икосаэдр, который искривлен, в результате чего его симметрия понижается.
Икосаэдр Йессена	Если у объемного геометрического тела 12 граней, каждая из которых представляет собой равнобедренный треугольник, и расположены эти грани таким образом, что образуют невыпуклое тело, то эта фигура уже будет называться икосаэдром Йессена (или ортогональным икосаэдром). У него прямые 2-гранные углы. Одна из его особенностей заключается в том, что он равносоставлен с шестигранником, каждая грань которого представляет собой квадрат. Это означает, что его можно разделить на небольшие многогранники, а из них затем составить шестигранник с равными по величине гранями. Такой шестигранник является кубом.

Разузнай! — Как сделать икосаэдр своими руками — 3 способа

Икосаэдр – один из видов правильных многогранников. Он имеет выпуклую форму и характеризуется наличием 20 одинаковых граней, которые представляют собой равносторонние треугольники.

Помимо этого данная объемная фигура содержит 12 вершин и 30 ребер. Название фигуры в переводе с греческого означает «двадцать оснований».

Такое имя фигуры полностью характеризует ее структурные особенности.

Подобные геометрические объекты редко встречаются в быту, поэтому наблюдать их можно лишь в каких-то игральных элементах, кристаллах разных минералов и в молекулярных соединениях. Также существует мнение, что данная фигура является более точной передачей форм Земли и некоторых планет.

Как сделать икосаэдр

Существует множество разнообразных, но простых способов, которые позволяют воссоздать икосаэдр собственными руками. Это позволит наглядно оценить всю таинственность и сложность данной фигуры.

Способ №1 Икосаэдр из готового макета

Первый способ сводиться к тому, чтобы найти в сети изображение развертки фигуры и подать ее на печать. После этого вырезать по конуру и сложить в соответствии с указанными линиями сгиба. Для предания большей эффективности, полученную фигуру можно разукрасить и покрыть лаком. Это позволит не только сделать икосаэдр более ярким и эффектным, но и продлить срок его жизни.

Способ №2 Как сделать икосаэдр вручную

Можно сделать модель икосаэдра и без дополнительных материалов. Для этого понадобиться бумага, карандаш и линейка.

При помощи линейки рисуем очертания – для этого нужно изобразить набор треугольников либо для упрощения прямоугольников. Должна получиться фигура, напоминающая перекошенную стопку блоков или домино.

После этого вырезаем самодельный шедевр и складываем икосаэдр. Для наглядности можно использовать следующую схему. Она, кстати, подойдет и для первого способа.

Способ №3 Икосаэдр из полимерной глины – горшок для цветов

Данную фигуру можно легко использовать для создания интересных в плане дизайна вещей, например, горшка для цветов. К списку требуемых во втором способе инструментов, добавим полимерную глину и можно начинать изготовление. Из куска бумаги вырезаем треугольник.

Его размеры зависят от размеров желаемого горшка. Далее по форме этого треугольника укладываем глину. Должно получится 15 глиняных треугольников. Далее складываем их в форме икосаэдра, верхнюю часть, оставляя пустой. Далее в нижней части, пока глина мягкая, делаем отверстия для стекания воды.

Их не нужно слишком много. После этого крепим ножки, которые также изготавливаем из глины и отправляем наш горшок для цветов в печь. Там он приобретет достаточной прочности и будет радовать вас и ваших гостей.

Таким же способом можно изготовить подсвечник или этажерку. В общем, все ограничивается только фантазией.

Как сделать икосаэдр из бумаги?

Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда. Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.

Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.

Как сделать икосаэдр из бумаги: схема

Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:

макет икосаэдра;
клей ПВА;
ножницы;
линейка.

Распечатываем на листе бумаги макет икосаэдра.
Вырезаем его по пунктиру. Это необходимо для того, чтобы было свободное место для склеивания деталей между собой

Важно как можно более медленно вырезать икосаэдр, поскольку при малейшем сдвиге поделка будет в итоге выглядеть некрасиво. Такая необходимость в более аккуратном вырезании обусловлена тем, что все треугольники в икосаэдре имеют одинаковые стороны, и если какая-то сторона будет отличаться по своей длине, в итоге такое расхождение в размерах будет бросаться в глаза

Складываем икосаэдр по сплошным линиям.
С помощью клея проклеиваем места, очерченные пунктирной линией, и соединяем между собой соседние стороны треугольников. Необходимо подержать в таком состоянии каждую проклеенную сторону в течение 20 секунд для более плотной фиксации. Аналогичным образом нужно проклеить все стороны икосаэдра. Наибольшую сложность в склеивании представляют два последних ребра, поскольку для их соединения требуется сноровка и терпение. Икосаэдр готов.

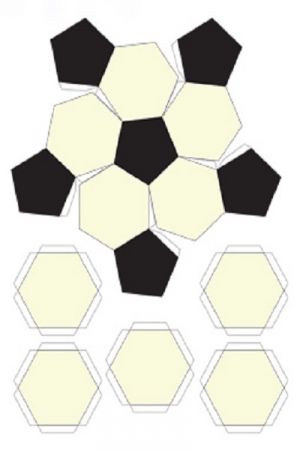
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку. Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч

Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч

Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч

Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.

Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:

Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.

Правильные и неправильные звездчатые многогранники

Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.

Как сделать многогранник из бумаги: второй способ

Изготовьте два главных шаблона (фото 5):

— Первый.

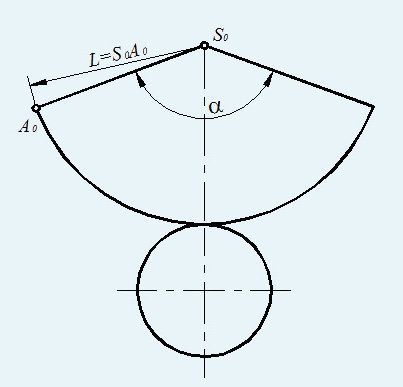
Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.

— Второй.

Этот шаблон — пятиконечная звезда. Выполните одинаковые двенадцать заготовок. Формируя многогранник, каждую из звезд с подогнутыми вверх концами помещают внутрь конусообразных деталей и приклеивают к граням.

Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.

Как сделать многогранник?

Необходимость сделать многогранник возникает нечасто, однако случается, что ребёнку на дом задают это задание или вы решаете сделать оригинальный подарок другу. А возможно, у вас возникла какая-то дизайнерская задумка. Так или иначе, понадобился многогранник из бумаги. Как его склеить?

Бумажная модель

Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:

Сложить листок пополам и сделать складку вдоль сгиба. Если используется бумага для оригами, то стоит убедиться, что её лицевая сторона находится снаружи, поскольку она будет видна позже.
Развернуть квадрат.
Сложить правую и левую стороны листа так, чтобы они встретились в месте сгиба. Должен получиться прямоугольник, больше похожий на шкаф с распашными дверцами.
Перевернуть фигуру подогнутыми краями вниз.
Сделать диагональную складку: верхний правый угол должен встретиться с левой стороной прямоугольника. Нужно свернуть обе «двери шкафа».
Перевернуть бумагу прямым концом вверх.
Сделать ещё одну диагональную складку, где верхний правый угол будет встречаться со стороной макета. Должен получиться параллелограмм.
Согнуть лист по диагонали там, где верхний угол соответствует правому углу фигуры.
Повторить действие с другой стороны. Должны встретиться нижний и левый углы. Получится маленький квадрат.
Затем повернуть заготовку так, чтобы фигура напоминала ромб.
Сложить квадрат пополам, сделав сгиб, который идёт перпендикулярно «дверцам шкафа», видимым на модели. Итак, первая единица готова.

Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.

Кусудама из правильных пятиугольников

Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.

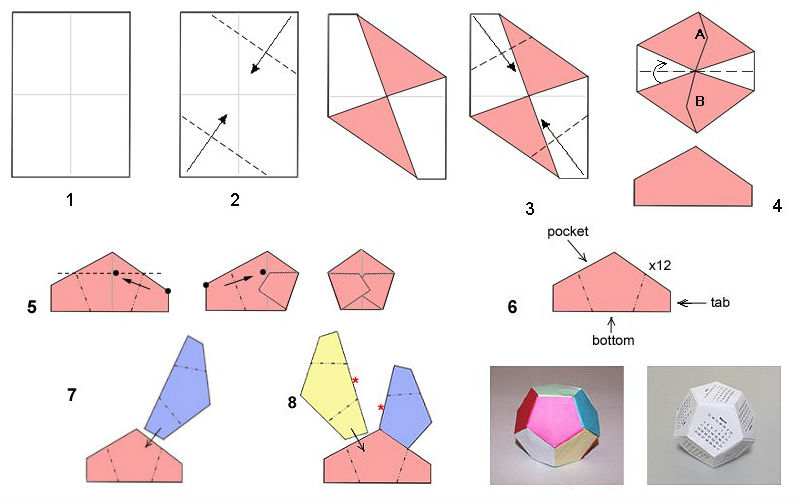
Пошаговая инструкция:

Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
Аналогично складываем противоположные углы.
Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
Продолжаем сборку, пока не используем все 12 модулей.

Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Виды треугольников:

Прямоугольный. Один угол прямой, два других менее 90 градусов.
Остроугольный. Градус угла больше 0, но меньше 90 градусов.
Тупоугольный. Один угол тупой, два других острые.

Свойства треугольника:

В треугольнике против большего угла лежит большая сторона — и наоборот.
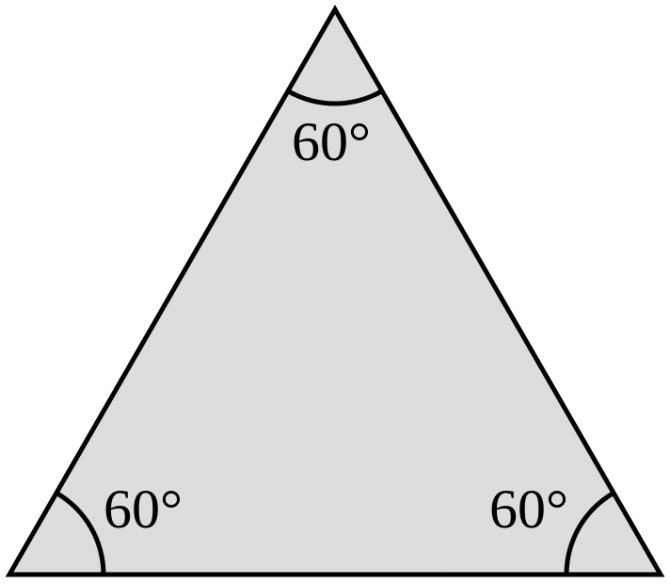
Сумма углов треугольника равна 180 градусов.
Все углы равностороннего треугольника равны 60 градусам.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

Если известна сторона и высота. S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:
Если известны две стороны и синус угла. S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
Если есть радиус описанной окружности. S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
Если есть радиус вписанной окружности. S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Как построить развертку самостоятельно?

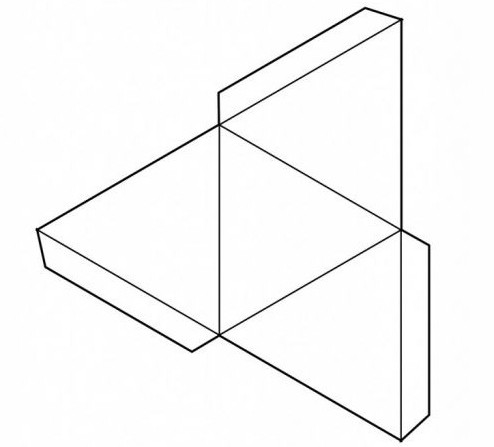
Пожалуй, помимо склеивания многогранника — хоть звездчатого, хоть платоновского, — еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр — это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр — простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней — равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр — это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.

Делаем многогранник из бумаги

Для того, чтобы процесс работы было проще описать, расскажем, как сделать из бумаги треугольную пирамиду или тетраэдр ABCD. Это фигура с четырьмя гранями в виде равносторонних треугольников. Для работы нам понадобятся:

Сначала рисуем на бумаге ближе к нижнему краю листа (но не на самом краю!) основание тетраэдра — равносторонний треугольник ABC. Удобнее будет нарисовать его вершиной вниз, но это не принципиально.

Чтобы треугольник получился действительно равносторонним, лучше всего воспользоваться линейкой и циркулем. Рисуем прямую, на ней отсекаем отрезок AB, равный стороне треугольника. Точки А и В будут двумя вершинами треугольника. Затем циркулем рисуем две дуги такого же точно размера с центрами в точках А и В. В месте пересечения дуг будет третья вершина С.

Если не хотите работать с циркулем, можно воспользоваться транспортиром. Углы в равностороннем треугольнике равны 60 градусам. Из точек А и В рисуем лучи под углом 60 градусов к отрезку. Точка их пересечения будет вершиной С.

Основание есть. Теперь к нему нужно пририсовать ещё три таких же точно треугольника — боковые грани тетраэдра. Принцип построения треугольников остаётся тем же самым, только в качестве основания новых треугольников-граней возьмём уже нарисованные

стороны АВС. У нас получатся ещё три треугольника: АВD`, ВСD« и САD«`.

Нам нужно будет собрать все три вершины D`, D«, D«` в одну точку D и склеить фигуру. Для склейки потребуется пририсовать дополнительные полоски бумаги примерно по 0,5 см шириной к сторонам А D`, В D« и С D«`.

Теперь можно вырезать получившуюся фигуру, согнуть её аккуратно по всем линиям, намазать клеем дополнительные полоски и склеить.

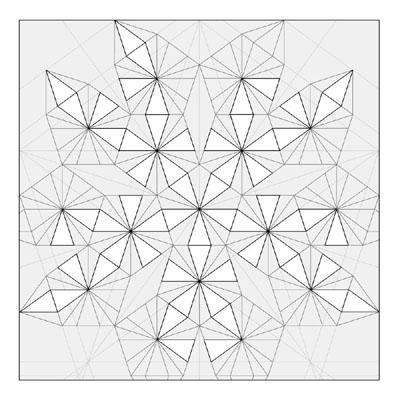
Развёртку более сложных фигур делают точно так же. Но если не хочется думать самому, в интернете можно найти готовые. Например, вот изображены развёртки сразу нескольких фигур.

Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра. Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер). Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань). Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и ). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.

Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами. Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости. Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения. Выдвинутая еще во времена Платона версия о том, что Вселенная представляет собой огромного размера додекаэдр, нашла подтверждение уже в начале XXI -го века. После тщательного анализа данных, полученных при помощи WMAP(многофункционального космического аппарата NASA), ученые согласились с предположением древнегреческих астрономов, математиков и физиков, в свое время занимавшихся вопросами изучения небесной сферы и ее строением. Более того, современные исследователи считают, что наша Вселенная представляет собой бесконечно повторяющийся набор додекаэдров.

Занимательные грани

Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела — выпуклые многогранники, состоящие только лишь из Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то
развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.

Построение чертежа

Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.

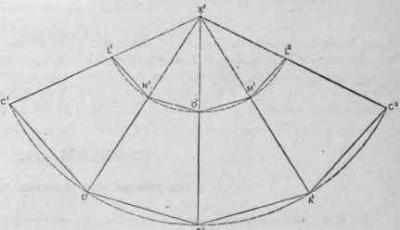
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.

Самые популярные скульптуры

От простого декора переходим к наиболее востребованным сегодня полигональным изделиям – фигурам животных

Они прекрасно вписываются в интерьер современного стиля, сразу привлекая внимание и вызывая восхищение. Проще всего использовать для работы готовые шаблоны, однако можно сделать их и самостоятельно в профессиональных программах 3ds max или Blender

Если хочется проявить творческий подход, начинать следует с поиска референсов – фотографий животных в хорошем качестве и, желательно, сделанных с разных сторон

На этом этапе важно определиться с позой и пропорциями модели, а также решить, должна ли она быть максимально реалистичной или стилизованной. Только выполнив художественную часть, приступают к технической – построению по референсам 3D-модели и разбивке её с помощью полигональной сетки

Существует три типа скульптур low-poly: целые фигуры, маски и трофеи. Последний вариант актуален для сканди-интерьеров. Трофеи – полигональные скульптуры в виде головы животного, закреплённой на стене, словно добыча охотника. Чаще других изображают медведя, лису, волка, быка, слона и единорога. Но безусловным лидером этого топа можно назвать оленя, который занимает особое место в скандинавской мифологии. Издревле он считался посланником богов и, по убеждению северных народов, обладал исцеляющей силой.

Олень

Есть несколько вариантов оленя в стиле паперкрафт. Однако развёртка даже самого простого из них впечатляет количеством деталей.

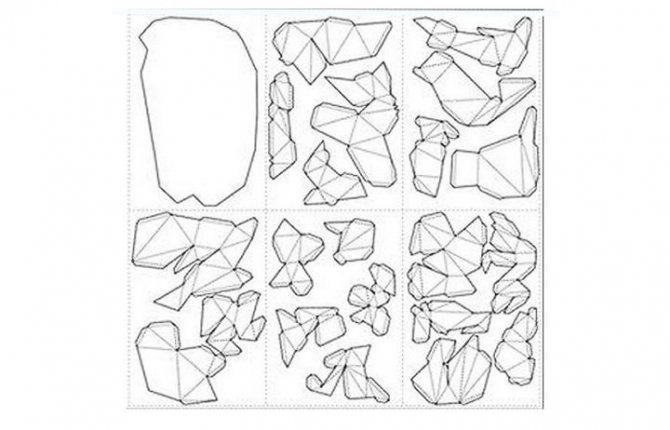
Ещё эффектнее выглядит голова оленя – охотничий «трофей». Паперкрафт-развёртка и пошаговая инструкция по сборке представлены в видео-уроке, там же есть ссылка на шаблон для скачивания:

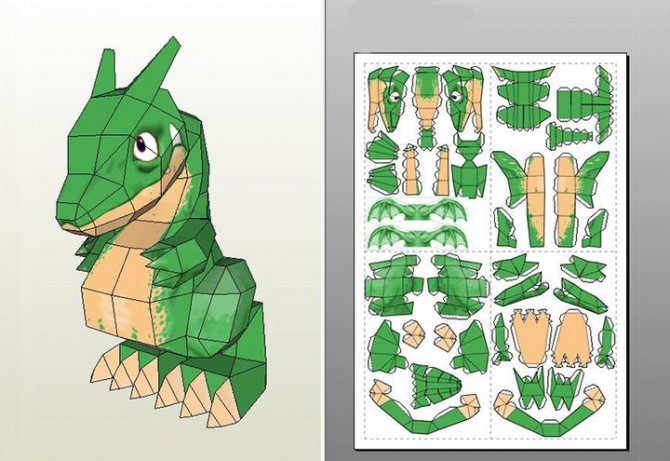
Дракон

Мифические крылатые химеры словно созданы для паперкрафта. Что подтверждает развёртка дракона, вполне доступная для сборки с детьми:

Лиса

Лисы занимают второе место по популярности после оленей. Разработаны сидящие, стоящие, спящие модели и даже забравшиеся на луну. Есть паперкрафт в виде головы лисы – развёртка для неё приведена ниже:

Современное использование додекаэдра

В настоящее время геометрические объекты в форме додекаэдра находят применение в некоторых сферах деятельности человека:

Игральные кости для настольных игр. Так как додекаэдр — это платоновская фигура, обладающая высокой симметрией, то объекты этой формы можно использовать в играх, где продолжение событий имеет вероятностный характер. Игральные кости в своем большинстве изготавливают кубической формы, поскольку их сделать проще всего, однако современные игры становятся все сложнее и разнообразнее, а значит, требуют костей с большим количеством возможностей. Кости в форме додекаэдра применяются в ролевой настольной игре Dungeons and Dragons. Особенностью этих костей является то, что сумма цифр, расположенных на противоположных гранях, всегда равна 13.

Источники звука. Современные звуковые колонки часто изготавливают в форме додекаэдра, поскольку они распространяют звук во всех направлениях и защищают его от окружающего шума.

Схемы для вырезания

Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.

Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).

Шара

Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.

Материал, из чего можно сделать плотный шар — картон или плотная бумага.

https://youtube.com/watch?v=EFz1XRfr_WI