Как сделать пирамиду из бумаги. Пошаговая инструкция
Благодаря древнему мастерству оригами есть возможность воссоздавать практически любую фигуру из бумаги, в том числе и пирамиду. Существует несколько способов, как создать идеальную фигуру с четкими гранями. Для новичков в этом деле есть легкий пошаговый совет, как сделать фигуру из картона. Данная инструкция будет понятна как взрослым, так и детям.
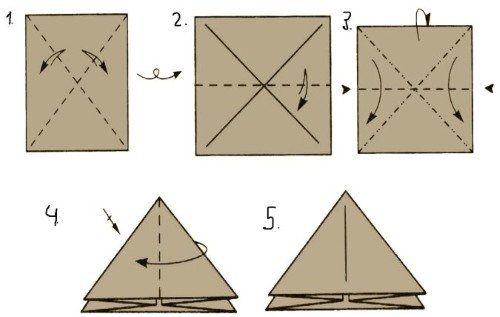
Пошаговое руководство, как склеить пирамиду из картона:
- На бумажном листе нужно нарисовать один ровный квадрат и три треугольника. Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см.
- Ножницами вырезать заготовки не по контуру, а с отступом 3-4 мм, в дальнейшем это будет необходимо при склеивании фигуры.
- Смазать клеем все части, дать ему немного подсохнуть и сложить все детали в единую конструкцию.
- Дать полностью высохнуть поделке и можно приступить к декору.
Как украсить пирамиду — может быть любая воля фантазии. Например, на нее можно наклеить фигурки, обмотать фольгой или раскрасить специальными акриловыми красками.
Материалы и приспособления
Как сделать пирамиду из бумаги схема с размерами – не единственные главные составляющие в изготовлении фигуры.
Для удобства выполнения оригами следует заранее подготовить необходимые материалы и приспособления, чтобы в момент работы все они были под рукой:
- Для изготовления граней могут понадобиться различные материалы. Задействовать можно не только картон, но и пластик, металл, фанеру, стекло или сделать каркас из проволоки. Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией.
- Для поделки стоит обзавестись качественным клеем, который можно купить в канцелярском магазине.
- Пригодятся острые ножницы, чтобы вырезать ровные заготовки для будущей фигуры.
- Также нужны будут линейка, карандаш и ластик на всякий случай.
Для выполнения фигуры не требуется много материалов, все приспособления для пирамиды найдутся почти в каждом доме.
Определяем параметры
Чтобы изделие получилось аккуратным и красивым стоит задать четкие параметры при изготовлении заготовок для будущей пирамиды. Для каждой части может понадобиться отдельный лист бумаги. Можно скачать уже готовые схемы, но их также просто нарисовать самостоятельно.
Высоту геометрической фигуры можно выбрать любую, но рекомендуемая длина, чтобы она была больше на 10-15 см ширины заготовки. Именно при таком соотношении фигура будет смотреться гармонично.
Строим чертеж
Чтобы было проще узнать, как сделать идеальную пирамиду из бумаги или каких-либо других материалов существует схема с размерами. Чертеж – основа для дальнейшего склеивания компонентов для будущей цельной фигуры. Существует несколько видов пирамид, для каждой из них свой чертеж.
Но есть один простой способ, который подходит для детей и новичков в этом деле:
- В основании пирамиды должен быть правильный многоугольник, с проходящий высотой через его центр. Заранее стоит определить размеры пирамиды, для каждого они могут быть индивидуальны.
-
Нужно нарисовать четыре квадрата, три из них будут нужны для треугольников.
- На одной из боковых сторон нужно определить середину линии. От двух углов основания следует провести две линии в отмеченную точку, чтобы получилась вершина пирамиды.
- Заготовки равнобедренных треугольников нужно будет соединить с квадратом с помощью специальных отступов. Стоит не забыть, что вырезать заготовки нужно прибавив к их краям полсантиметра для того чтобы было удобно склеить фигуру.
Завершение моделирования
Вырезанную фигуру, нужно склеить по линиям сгибов. Перед тем как соединить части в полную модель на сгибы нужно нанести клей и немного оставить его застыть, чтобы он лучше схватился. После того как изделие будет готово следует его оставить на полчаса, чтобы потом при оформлении оно случайно не расклеилось. В завершающий этап моделирования входит дизайнерское оформление работы.
Изделие можно обклеить фольгой или бумагой для подарков. Также для тех, кто верит в мистическую силу пирамиды стоит на нее приклеить натуральные камни, которые будут подходить под знак зодиака того, кому будет подарена данная фигура. В детском варианте пирамиду можно превратить в животное, приклеив к ней ушки, хвостик и нарисовать черты мордочки.
Как из бумаги сделать тетраэдр?
Тетраэдр – самая простая фигура из многоугольников. Он состоит из четырех граней, каждая из которых представляет собой равносторонний треугольник, при этом каждая из сторон соединяется с другой всего лишь одной гранью. При изучении свойств этой трехмерной геометрической фигуры для наглядности лучше всего сделать модель тетраэдра из бумаги.
Как склеить тетраэдр из бумаги?
Для построения простого тетраэдра из бумаги нам понадобится:
- собственно бумага (плотная, можно использовать картон);
- транспортир;
- линейка;
- ножницы;
- клей;
- тетраэдр из бумаги, схема.
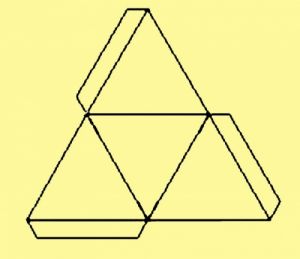
- Работу над тетраэдром начинаем с рисования развертки из бумаги. Если выполнение фигуры планируется из обычной бумаги, можно чертить развертку прямо на ней.
- Чертим прямую, которая будет являться гранью тетраэдра. С двух концов откладываем углы по 60 ⁰ , а через полученные точки проводим прямые линии до их пересечения. У нас получился равносторонний треугольник.
- Далее на каждой стороне полученного треугольника строим такие же. От каждого конца снова откладываем по 60 ⁰ и соединяем. В результате должна получиться схема, состоящая из четырех равносторонних треугольников.
- Для того, чтобы развертку можно было склеить и получить тетраэдр, следует сделать припуски по 1 см с трех сторон разных треугольников. В результате получается вот такой чертеж .
- Вырезаем развертку и сгибаем ее по всем линиям, припуски загибаем внутрь, если нужно, обрезаем углы. Мажем их клеем и прижимаем ко внутренним сторонам граней, состыковав линию сгиба между стороной и припуском со стороной свободного треугольника.
Несколько дополнительных рекомендаций:
- если бумага очень плотная, то по местам сгибов следует провести твердым предметом, например, ребром линейки;
- для того, чтобы получить разноцветный тетраэдр, можно раскрасить грани или выполнить развертку на листах цветной бумаги.
Как из бумаги сделать тетраэдр без склеивания?
Предлагаем вашему вниманию мастер-класс, в котором рассказывается, как собрать 6 тетраэдров из бумаги в единый модуль при помощи техники оригами.
- 5 пар квадратных листов бумаги различных цветов;
- ножницы.
- Каждый лист бумаги делим на три равные части, разрезаем и получаем полосы, соотношение сторон в которых 1 к 3. В результате получаем 30 полос, из которых и будем складывать модуль.
- Кладем полосу пред собой лицевой стороной вниз, вытянув по горизонтали. Сгибаем пополам, разворачиваем и подгибаем к середине края.
- На дальнем правом краю сгибаем угол так, чтобы сделать стрелку, поведя ее на 2-3 см от края.
- Аналогичным образом сгибаем левый угол (фото как из бумаги сделать тетраэдр 3).
- Перегибаем правый верхний угол маленького треугольничка, который получился в результате предыдущей операции. Таким образом, боковые стороны сложенного края окажутся под одинаковым углом.
- Разворачиваем полученную складку.
- Разворачиваем левый уголок и по уже имеющимся линиям сгиба заворачиваем угол внутрь как показано на фото.
- В правом углу сгибаем верхний край вниз таким образом, чтобы он пересекся со складкой, сделанной во время операции №3.
- Внешний край еще раз заворачиваем направо, используя складку, выполненную в результате операции №3.
- Предыдущие операции повторяем с другого конца полоски, но так, чтобы маленькие складочки оказались на параллельных концах полоски.
- Полученную полоску складываем пополам по длине и даем ей немого раскрыться самопроизвольно. Точный угол раскрытия станет понятен потом, при окончательной сборке модели. Элемент готов, теперь аналогичным образом делаем еще 29.
- Звено переворачиваем таким образом, чтобы во время сборки была видна его внешняя сторона. Соединяем два звена, вставив язычок в кармашек, образованный маленьким внутренним углом.
- Соединенные звенья должны образовывать угол в 60 ⁰, под которым будут присоединяться и другие звенья (фото как из бумаги сделать тетраэдр 13).
- Добавляем третье звено ко второму, а второе соединяем с первым. Получается конец фигуры, на вершине которой соединяются все три ее звена.
- Аналогичным образом добавляем еще три звена. Первый тетраэдр готов.
- Углы у готовой фигуры могут быть не совсем одинаковыми, поэтому для более точной подгонки следует оставлять открытыми отдельные углы всех последующих тетраэдров.
- Между собой тетраэдры следует соединять так, чтобы угол одного проходил сквозь отверстие в другом.
- Три соединенных между собой тетраэдра.
- Четыре соединенных между собой тетраэдра.
- Модуль из пяти тетраэдров готов.
Если вы справились с тетраэдром, можно продолжить и смастерить из бумаги призму, икосаэдр, параллелепипед и другие геометрические фигуры.
Сборка основы тетраэдра
Для сборки основы тетраэдра из бумаги вам потребуется:
— Кусок бумаги нужного размера;
— Схемы для сборки тетраэдра;
Шаги по сборке:
1. Начните с создания кластера из четырех равных треугольников. Это будет основа вашего тетраэдра.
2. Следуйте схемам, чтобы правильно собрать основу, совмещая стороны треугольников и приклеивая их края бумагой или клеем.
3. Убедитесь, что основа тетраэдра крепкая и надежно собрана.
4. Проверьте, чтобы все углы основы были равными и треугольники были ровными.
5. По завершении этой части сборки, вы получите основу тетраэдра, готовую к продолжению создания его боковых сторон.
Подробнее о сборке тетраэдра можно узнать из видео и фотоинструкций.
Складывание основы тетраэдра
Как сделать тетраэдр из бумаги? Это совсем не сложно! В этом разделе мы покажем вам пошаговую схему, которая поможет вам создать основу тетраэдра своими руками.
Фото и видео материалы также будут полезны вам в процессе создания.
Чтобы сделать основу тетраэдра, вам понадобится 4 равнобедренных треугольника. Складывайте их по схеме, соединяя стороны треугольников между собой.
Когда все треугольники собраны вместе, вы получите кластер, который должен выглядить, как будто он составлен из треугольных граней тетраэдра.
Важно: следите за правильным соединением сторон треугольников, чтобы ваш тетраэдр был устойчивым и гармоничным. Теперь, когда вы сделали основу тетраэдра, вы можете переходить к следующему этапу — сборке остальных граней и приданию формы уже готовому тетраэдру. Теперь, когда вы сделали основу тетраэдра, вы можете переходить к следующему этапу — сборке остальных граней и приданию формы уже готовому тетраэдру
Теперь, когда вы сделали основу тетраэдра, вы можете переходить к следующему этапу — сборке остальных граней и приданию формы уже готовому тетраэдру.
Удачи в своем творчестве!
Крепление элементов основы
Когда все четыре грани основы тетраэдра сделаны и готовы, настало время приступить к их креплению. Это важный этап, ведь от правильного крепления зависит прочность и устойчивость конструкции.
Сначала необходимо собрать кластер из трех граней основы. Для этого возьмите одну из граней и аккуратно приклейте по нижним краям две другие грани, образуя треугольник. Чтобы грани хорошо держались, можно приклеить их с обратной стороны с помощью скотча. Убедитесь, что грани плотно соприкасаются и углы треугольника равны.
После этого вставьте полученный кластер в одну из четырех щелей на верхней грани основы. Затем, края пустых щелей можно закрыть оставшимися гранями. Приклейте их, убедившись, что все детали установлены правильно и не кривятся.
Повторите эту процедуру для всех оставшихся граней основы. Приклейте их к уже собранным кластерам и закрепите между собой, пока не получится полноценный тетраэдр. Не забудьте проверить стыки и при необходимости скорректировать их, чтобы все грани были ровны и основа выглядела аккуратно.
После завершения сборки основы, можно приступить к добавлению дополнительных деталей, например, украшений или аппликаций. Не забывайте фиксировать их к основе с помощью клея или другого подходящего способа крепления.
Теперь вы знаете, как самостоятельно сделать тетраэдр из бумаги! Следуйте нашим подробным инструкциям, используйте фото, видео и схемы для лучшего понимания процесса. И не забывайте быть аккуратными и терпеливыми — ведь результат стоит того!
Особенности работы с геометрическими фигурами в разном возрасте
Поделки из фигур доступны для занятий с детьми с самого младшего возраста.
Для малышей 2-4 лет задание не должно включать в себя больше 5 деталей
В противном случае ребенок быстро устает, путается, а внимание его рассеивается. Для изготовления поделки малышу необходимо приготовить готовые элементы поделки из цветной бумаги и предложить основу с готовым контуром. Или показать, последовательность выполнения работы
Дети в возрасте 4-5 лет могут вырезать из бумаги простые детали самостоятельно, но под присмотром взрослых. Для работы ребенку необходимы ножницы с закругленными концами. Дети такого возраста способны сами выполнить поделки средней сложности. Учащиеся младших классов справляются самостоятельно с достаточно сложными заданиями
Или показать, последовательность выполнения работы. Дети в возрасте 4-5 лет могут вырезать из бумаги простые детали самостоятельно, но под присмотром взрослых. Для работы ребенку необходимы ножницы с закругленными концами. Дети такого возраста способны сами выполнить поделки средней сложности. Учащиеся младших классов справляются самостоятельно с достаточно сложными заданиями.

Для того, чтобы заинтересовать ребенка изготовлением поделки из геометрических фигур, можно предложить ему интерактивную игру на основе сказки “Мышонок и карандаш”. Затею эту можно осуществить в домашних условиях на занятиях в детском саду. Необходимо заранее приготовить элементы, из которых состоит кошка: круги, овалы и треугольники.

Увлекательная игра поможет сделать творческий процесс интереснее для очень активных детей.

Плоские геометрические фигуры из бумаги – Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
“Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них”, – взрослый показывает одну или две игровых схемы замка с нашего задания. – “Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.” – взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку
И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Тонкости работы
Построить разверту многогранника и склеить из нее бумажную модель — дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.

Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение — детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.
Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.

Большой тетраэдр из картона
Тетраэдр из картона (сделать поэтапно можно по инструкции, представленной далее в статье) получится крепким и будет хорошо держать форму. Размер объёмной фигуры зависит от вида картона.
Какой картон можно использовать для работы:
Не цветной картон после сборки тетраэдра можно покрасить или обклеить бумагой с узорами. Если на грани небольшой фигуры наклеить календарные листы или фотографии, можно получить необычное украшение для рабочего стола.
Особенности работы с жестким картоном
Тетраэдр из картона (сделать поэтапно развертку можно, не используя шаблоны) изготавливают следуя этим правилам:
Удобнее всего работать с двухслойным гофрированным картоном. Его можно вырезать из большой коробки, в которой перевозят бытовую технику. С картоном, сложенным в 3 и более слоя, работать будет намного сложнее. Такой материал плохо гнется и тяжело склеивается.
Подготовка и вырезание шаблона
Тетраэдр из картона (сделать поэтапно можно за 1 ч) можно изготовить, используя любой вид развертки. В этом мастер-классе описан процесс составления круговой развертки, без использования шаблона.
Порядок действий:
- В центре картонного листа начертить горизонтальную линию, длина которой будет равна размеру ребра фигуры.
- К левому концу линии приложить транспортир. Отметить 60 градусов.
- Приложить транспортир к правому концу линии. Отметить 60 градусов.
- Через отметки провести 2 линии до их пересечения. Должен получиться равносторонний треугольник.
- От вершины треугольника, отложить 60 градусов с левой стороны. Начертить новый треугольник сбоку. 1 его сторона станет общей с уже начерченной фигурой.
- Приложить транспортир к основе 1 фигуры. Отметить 60 градусов с обоих концов. Провести линии. Получилась 3 грань тетраэдра.
- Последнюю грань начертить по аналогии, приложив транспортир к правой стороне нижнего треугольника.
- на нижней стороне треугольника слева;
- на левой стороне верхнего треугольника;
- На правой стороне треугольника, расположенного справа.
Вырезать развертку канцелярским ножом.
Соединение граней
Как соединить грани фигуры:
Дождаться полного высыхания клея. Если остались излишки (застывшие капли или паутинки), их можно аккуратно срезать канцлерским ножом.
Научиться делать тетраэдр из бумаги или картона помогут инструкции, где все действия расписаны поэтапно. Главное, составить точный чертеж, а затем аккуратно вырезать развертку, используя подходящие инструменты.
Давно давно тоже хочу. Спасибо Ира. После такой красоты обязательно соберу тоже! Класс!
Спасибо! Приятной сборки
Ир,а подскажи размер прямоугольника,а то в видео не понятно. и если можно,диаметр в конце сборки.
Спасибо, Танюша, что сподвигла меня раскопать этот многогранник и измерить его! Собирала давно, размеры подзабылись. А сейчас вот измерила: диаметр его около 17 см. А прямоугольники 5 на 15 см. (Добавлю теперь в начало поста ).
04:24
03:31
05:41
05:02
02:29
03:36
04:43
-
Как сделать из пластилина росомаха
-
Выставка поделок из пластилина глины соленого теста моя любимая чашка
-
Как сделать кубок из пластилина
-
Как сделать волосы из пластилина для скульптуры мальчика
- Игрушки как сделать перенос
Вырезание фигуры из бумаги по схеме
Прежде чем приступить к сборке, необходимо подготовить рабочее место. Затем, распечатайте заготовки. Следите за тем, чтобы детали были пронумерованы. В случае отсутствия номерков, собственноручно напишите их на полях. Это сэкономит время при склеивании крупных поделок. Существует три вида линий, согласно которым появляются заготовки. Сплошная линия — отрезать часть бумаги с помощью ножниц. Пунктирная линия — на моделях без текстур сгибается внутрь, с текстурами — наружу. Шрих-пунктирная — без текстур наружу, с текстурами – внутрь.
Заготовки вырезайте осторожно, не забывайте оставлять «клейкие поля». Благодаря им, различные части изделия будут соединяться друг с другом. Всё сгибайте по линиям сгиба
Если он очень длинный (более 8 см) то, пользуйтесь линейкой
Всё сгибайте по линиям сгиба. Если он очень длинный (более 8 см) то, пользуйтесь линейкой.
Техника безопасности
- Сухое место обезопасит от попадания ненужной влаги.
- Процесс склейки проводите за столом, а не где нибудь на диване или полу.
- Готовое изделия на краю стола, стеллажа, шкафа, обязательно упадет.
- Пыль с готового изделия вытирайте сухой тряпкой.
- Содержите рабочее место в порядке, так как труд очень кропотливый и лишний хаос в заготовках вам точно не нужен.
Пирамида — развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Куб
Давайте попробуем сделать куб. Предварительно подготовьте бумагу, клей, ножницы, линейку. Не забудьте распечатать схему (можно нарисовать самостоятельно). И обязательно запаситесь терпением, потому что первый раз самый сложный.
Поделка из бумаги в виде геометрической фигуры куб, является самым простым в исполнении многогранником. Здесь каждая сторона квадратная. Определяемся с размерами граней
Важно, чтобы ширина полотна была не меньше трех сторон квадрата, длина – не более пяти
Рисуем в длину 4 квадрата (боковые стороны куба должны быть вплотную по одной линии). Под квадратом и над ним изобразить еще по одному. Потом дорисовываются полоски, которыми стороны будут склеиваться.
Если что-то непонятно, можно посмотреть пошаговую инструкцию. Поделки из геометрических фигур из шаблонов, делать совершенно несложно. Все, куб готов.
Как сделать тетраэдр из картона
Правильный тетраэдр — простейший многогранник, гранями которого являются четыре правильных треугольника, треугольная пирамида. Также является одним из пяти правильных многогранников (Платоновы тела). У тетраэдра 4 грани, 4 вершины и 6 рёбер.

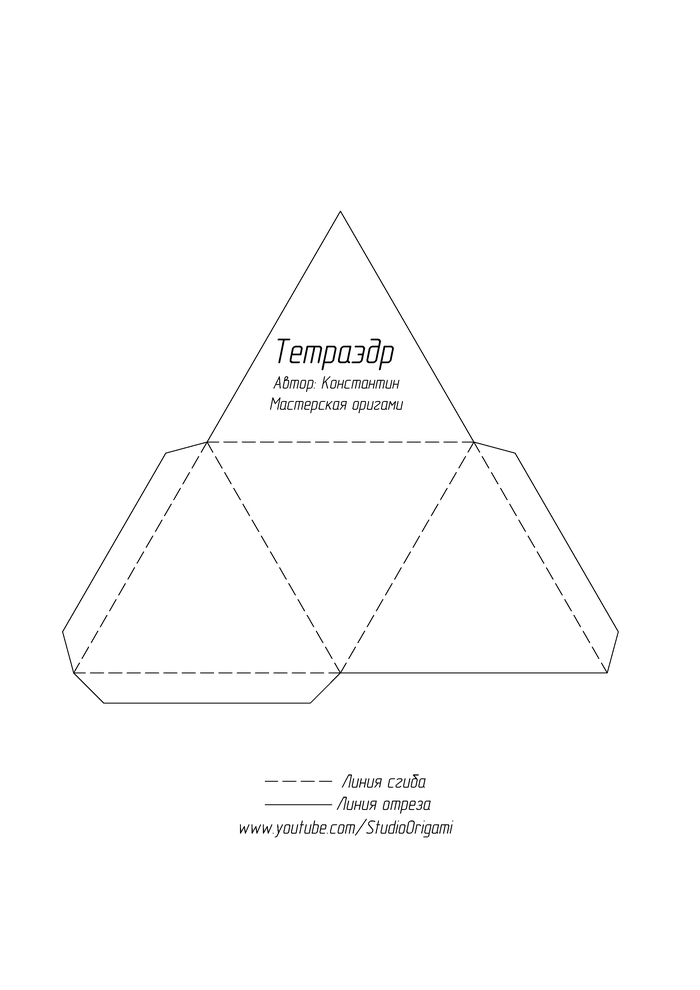
Если что-то непонятно, то можете посмотреть мою видеоинструкцию:
ну теперь охуеть!
может пора отдельный раздел на пикабу завести, наряду со «свежим», «лучшим» и «горячим» — «для альтернативно умных».
Я клапаны для склейки вообще делал отдельно — так грань получается более острой. Да, я задрот бумаги:). Для более легкого сгиба картона в зависимости от толщины естественно я с обратной стороны проводил тупым концом ножниц по линии как бы проминая верхний слой картона. Сгибается на ура!
Хм. Для восьмилетней девочки — очень даже.




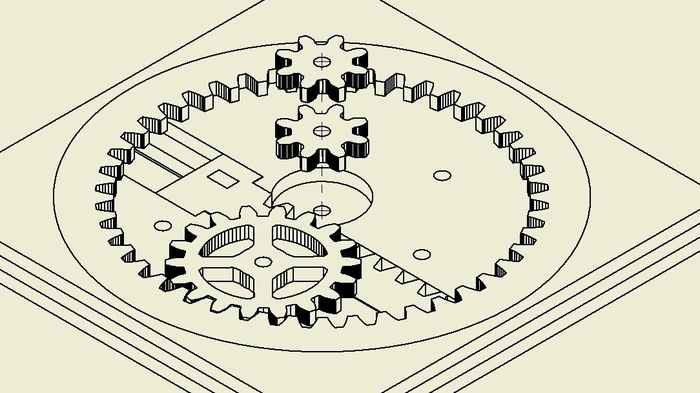
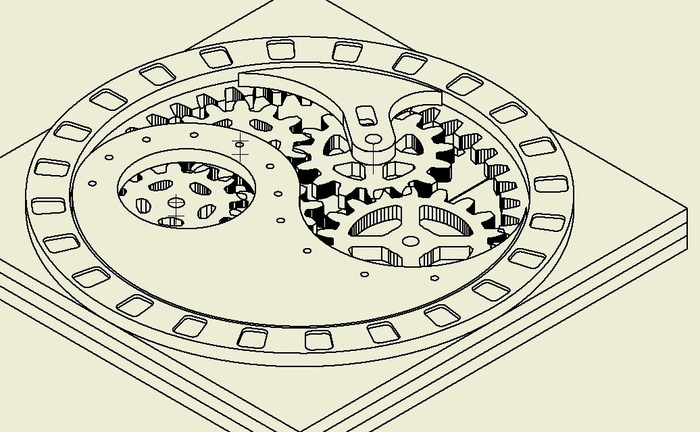
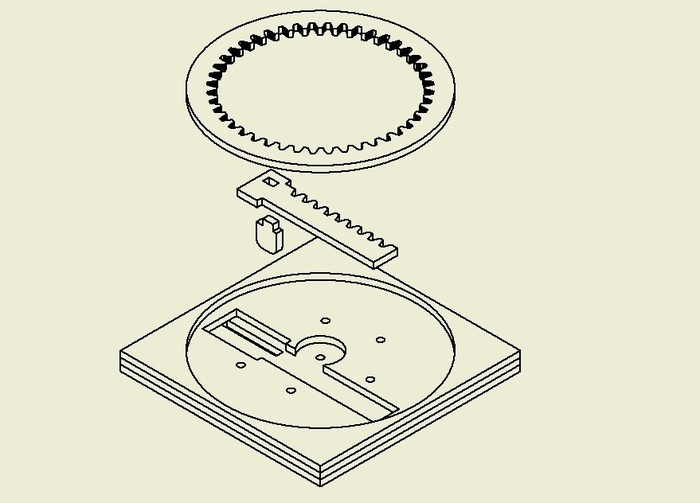


Меркаба (Куб Метатрона, звездчатый октаэдр)


Звездчатый октаэдр. Имеет вид двух разнонаправленных взаимопроникающих тетраэдров. Так же в разных культурах может называться Меркаба, Меркава, Куб Метатрона и т.д.
Существует масса интерпретаций на тему значения, символизма и назначения этой фигуры. По праву она является одной из самых многоликих фигур сакральной геометрии.
В разных традициях рукотворную Меркабу использовали как магическое средство исцеления больных, а также для защиты себя и своих близких от негативного программирования, сглаза, порчи. Присутствие Меркабы в помещении, якобы, полностью меняет энергетическую структуру и препятствует проникновению демонических сил. В доме Меркабу рекомендуется помещать перед окнами, напротив входной двери.
Так же одна из духовных школ дает следующее описание: «Меркаба человека представляет собой взаимодействие между собой трёх тел: физического, астрального и ментального. Физическое тело представляет собой роль статора. Тетраэдр направленный вверх должен вращаться по часовой стрелке, тетраэдр направленный вниз должен вращаться против часовой стрелки. При определённой скорости вращения тонких тел называемой критической, поле вокруг человека превращается в кристалл, который и называется активированной меркабой. Если в этом состоянии у человека активированы сверх способности и он владеет знаниями тонких планов, то с помощью своей меркабы он способен творить чудеса — перемещаться сквозь пространство, летать в воздухе, переходить в параллельные миры, летать на другие планеты в тонких телах и пр.
Прошу прощения (особенно у завзятых материалистов) за некоторый уход в мистицизм и эзотерику, если вдруг кому-то интересна более подробная информация в этом направлении — интернет ею насыщен в избытке.В конце концов, помимо описанных предполагаемых свойств, эта фигура может использоваться, как необычный и яркий элемент в интерьере) Может быть установлена на подставке на стол или полку, либо же подвешиваться и свободно вращаться от малейшего движения воздуха.
Каркас выполнен из дерева и окрашен, а использованные в заплетении нитки ярко сияют в свете ультрафиолетовых ламп (что видно на фото). Высота примерно 40смФото в обычном освещении и в ультрафиолете.
Интересные факты
Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.
Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.

В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.
Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.
Додекаэдр-звезда
Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.
Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.

Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
Что такое треугольный модуль
В основе элемента лежит прямоугольник, размером от 1/4 до 1/36 альбомного листа (формат А4). Соединяются готовые модули за счёт выступающих «уголков» и глубоких «карманчиков», по принципу штекерного разъёма. Плотное прилегание деталей обеспечивает прочность конструкции, но для большей надёжности лучше дополнительно «посадить» их на клей.
Перед тем как делать треугольники для модульного оригами, необходимо нарезать прямоугольные заготовки определённого размера. Допустимо одновременное использование нескольких «калибров»: более крупного для основных объёмов и мелкого – для изящного декора. Разделить лист на модули можно, опираясь на базовую форму «Дверцы». Для самого ходового элемента 1/16 потребуется:
Получить 1/32 несколько сложнее. Лист А4 сначала в поперечном направлении делят вдоль центральной оси, а затем каждую половину складывают в четыре раза. Получается вдвое больше полос, чем в предыдущем случае. Для продольного направления действия те же, что и при разметке модуля 1/16. В результате образуются прямоугольники, размером 5,3х3,7 см. Нарезать заготовки лучше всего канцелярским ножом, подложив под лист доску, ДВП или специальный макетный коврик.

Получить прямоугольники 1/32 можно и другим способом:
Модуль-треугольник
Сложить из прямоугольной заготовки треугольную деталь не составит никакого труда. Единственное «но» – таких элементов потребуется очень много, в среднем, на одну фигурку высотой 25 – 30 см около 1000 штук. Опытные мастера советуют по мере возможности пополнять запасы деталей, занимаясь другими делами. Например, во время просмотра любимого сериала или прогулки с ребёнком. После некоторой тренировки, складывать треугольники получается, даже не глядя.
Пошаговая инструкция:
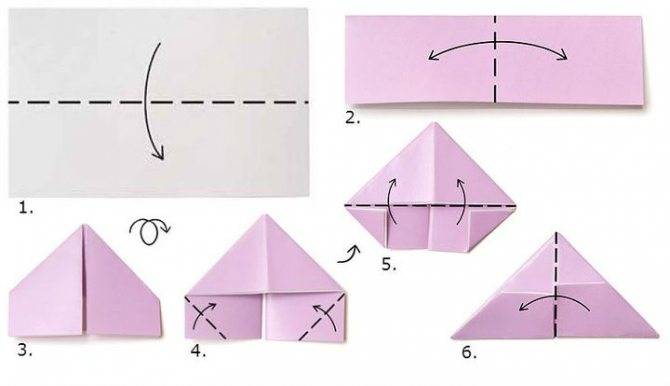
В итоге получаем классические треугольники для модульного оригами:

Существует несколько типов соединений модульных элементов. Они зависят:

Азбука модульного дела:






























